
掃碼添加微信�����,獲取更多半導體相關資料
引言
近年來�,復雜半導體制造設備的高效運行吸引了越來越多的研究興趣。該行業(yè)如今正處于增長擴張期�,這些市場的特點是高度科技化和充滿活力。這種現(xiàn)狀迫使晶圓制造工廠集中精力向客戶提供高質量��、價格合理的產(chǎn)品�����,同時縮短交貨時間和加工時間���。因此��,開發(fā)高效的短期調度策略成為達到競爭力的潛在替代方案��,靈活地響應高要求市場和客戶的要求��。自動濕法蝕刻站是現(xiàn)代半導體生產(chǎn)系統(tǒng)的關鍵部分����,它必須同時處理許多復雜的約束和有限的資源�。該站由一系列連續(xù)的化學和水浴以及共享的自動化批次轉移系統(tǒng)組成,其中必須嚴格遵循混合中間存儲策略��,以避免非常昂貴的晶圓污染����。
這項工作解決了半導體工業(yè)中最關鍵的階段之一,自動濕法蝕刻站(AWS)的短期調度問題����。開發(fā)了一種高效的基于MILP的計算機輔助工具,以實現(xiàn)順序化學和水浴的活動與有限的自動化晶片批次轉移設備之間的適當同步�����。主要目標是找到最佳的集成計劃�,最大限度地提高整個過程的生產(chǎn)率,而不會產(chǎn)生晶圓污染�����。
?
實驗
典型的晶圓制造工廠包括四個主要階段:制造����、探測����、組裝或包裝以及最終測試�。濕法蝕刻是在晶片制造階段進行的最復雜的操作之一。它利用晶片批次在預定順序的連續(xù)化學浴和水浴中的自動轉移���,在化學浴中有嚴格和確定的暴露時間(見圖1)�����。像機器人一樣��,自動化材料處理設備被用作在連續(xù)浴槽之間轉移批次的共享資源��。浴槽之間的轉移時間是確定的���。機器人不能在預定的傳送時間內保持一批晶片,也不能一次搬運一批晶片�。此外,化學浴遵循零等待存儲策略���,而水浴則允許本地存儲�����。
?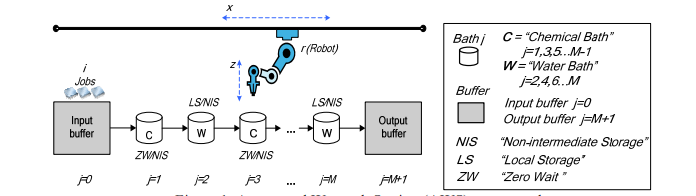
圖1 自動濕法蝕刻站工藝方案
浴槽一次只能處理一批�,過度暴露在化學物質中會嚴重損壞或污染晶圓。這種操作限制被稱為零等待和本地存儲策略��,在具有混合中間存儲策略的串行流多產(chǎn)品過程中成為自動濕法蝕刻站���。因此,通過應用混合中間存儲策略���,自動倉庫調度問題在物料處理和加工約束之間提供了復雜的相互作用����。
在這項工作中�,假設N個批次(i=1,2����,…,N)必須按照預先定義的配方進行處理��,這些配方指示了要訪問的浴池的順序�。此外,該問題考慮單個機器人可用,這假設所有批次在所有浴槽中必須遵循相同的順序(j=0��,1���,2�,…�����,M+1)�。因此,機器人的材料運動控制調度采用中心相關性����。
要面對的問題對應于在M個槽中的N個作業(yè)的調度,在具有ZW/LS/NIS策略的串行流多產(chǎn)品中���,共享資源具有有限的晶片移動能力�。
這項工作提出了一個嚴格的MILP數(shù)學公式的發(fā)展和應用��,以AWS調度問題��。它為在給定時間范圍內執(zhí)行的處理操作提供了最佳順序和時間����,同時確定了機器人的詳細拾取和傳送活動程序�����,主要目標是最大限度地減少完成所有晶圓批次所需的時間����。
?
結果和討論
我們對應于考慮四個連續(xù)浴槽NxM=[4x8]和八個晶片批次的AWS調度問題����。表1顯示了每個槽中每個晶片批次的處理時間以及預定的轉移時間����。為了分析傳輸時間對調度決策的重要性和影響,傳輸時間比原始案例研究大10倍����。
 ?
?
表1 槽j中的晶片批次處理時間和連續(xù)槽之間的轉移時間
我們測試了一個額外的解決策略,其中整個問題以順序方式解決���,這里稱為RCURM����。中心思想是首先使用URM模型解決問題,然后固定由URM模型獲得的生產(chǎn)順序��,并通過ORM公式解決詳細的機器人調度��。表2總結了模型統(tǒng)計數(shù)據(jù)��。這里值得注意的是����,URM模型僅明確考慮了預定義的轉移時間,假設機器人將始終可以執(zhí)行轉移操作���。在更受限制的情況下���,ORM模型還考慮了單個轉移移動設備的順序使用,這強制實施了洗澡時間表和機器人活動的適當同步���。通過查看最佳甘特圖�,我們可以很容易地觀察到��,在兩個問題實例的解決方案中都做出了相同的排序決策����。
?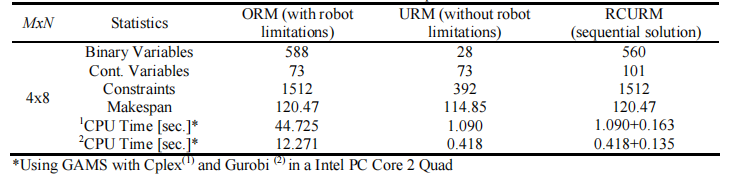
表2 模型統(tǒng)計和計算成本
因此�����,使用無限或單一機器人模型的事實將對排序決策產(chǎn)生直接影響�。?
通過分析模型統(tǒng)計數(shù)據(jù)�����,值得注意的是ORM和URM模型所需的二元變量和約束數(shù)量之間的顯著差異�����。模型大小的巨大差異主要是由于額外的排序約束和二元決策變量����,這些變量需要包含在MILP公式中��,以管理ORM固有的限制���。
?
總結
我們提出了一種新的MILP連續(xù)時間公式��,用于半導體工業(yè)中AWS過程的短期調度�。與典型的調度問題相反�,該模型能夠按照嚴格的中間存儲策略同時生成生產(chǎn)活動和轉移操作的詳細調度��。此外�����,還證明了所提出的模型可以很容易地用于以順序方式解決整個問題�����,即首先制定生產(chǎn)活動的時間表�,然后假設在第一步中定義的固定生產(chǎn)順序來求解轉移操作的時間表�。在所有的問題實例中,案例研究都是用很少的計算工作量得到最優(yōu)解決的��。未來的工作將集中于使用基于MILP的高效分解策略解決工業(yè)規(guī)模的問題��。